apuntes de Algebra
estructura de una expresión algebraica
SIGNO , COEFICIENTE , BASE , Y EXPONENTE
EXPRESIONES ALGEBRAICAS

notas
- cuando una expresión algebraica no tiene base { letra } no es expresión algebraica
- cuando una expresión algebraica no tiene exponente { numero de arriba } siempre va a hacer 1
- cuando una expresión algebraica no tiene signo siempre será positivo {+ }
- cuando una expresión algebraica no tiene coeficiente siempre será 1
- cuando una expresión algebraica no tiene exponente siempre será 1
- cuando un numero esta al cubo { 3 } se multiplicara 3 veces ese mismo numero
¿Qué es termino semejante ?
- termino semejante ; son expresiones cuya base y exponente son exactamente iguales
LENGUAJE COMUN Y LENGUAJE ALGEBRAICO
notas
lenguaje común
- dos numero
- la suma de dos números iguales
- la diferencia de dos números { resta }
- el producto de dos numeros { multiplicacion }
- el cociente de dos numeros { division }
- el triple de una hamburguesa
- la mitad de una torta
- la cuarta parte de una pizza
lenguaje algebraico
- A , B
A + A
X - Y
{ A } { B } A , B A * B
D ÷ i
2x
3h
T÷ 2
P ÷ 4
MONOMIOS
NOTAS
MONOMIOS
- termino con una expresión algebraica ; el grado de un monomio es igual a la suma de los exponentes de las bases de un monomio
- cuando no tiene exponente siempre valdra 1
- monomio viene de la terminación 1
- ¿como calcular el grado de un monomio ?
- -2a³ b² -------- 3+2= 5
a³ b² c d -------- 3 + 2+ 1+ 1 = 7
SUMA Y RESTA DE MONOMIOS
MULTIPLICACION Y DIVISION DE MONOMIOS
POLINOMIOS
polinomio
- termino con dos o mas expresiones algebraicas , el grado de un polinomio será igual al grado mayor de uno de los monomios que esta dentro del polinomio
- para saber el grado de un polinomio siempre se tomara al exponente mas grande
Suma y resta algebraica
- solo se podrán sumar o restar términos semejantes entre si sumando o restando los coeficientes y conservando la misma base y el exponente
suma de polinomios
- se identificaran términos semejantes y se sumaran o restaran los coeficientes de acuerdo a su signo y se conservaran las bases según su exponente
resta de polinomios
- el primer polinomio se copiara exactamente igual el signo menos multiplicara a cada uno de los términos del segundo polinomio se identificaran los términos semejantes y por ultimo se sumaran o restaran los coeficientes conservando base y exponente



MULTIPLICACION DE POLONOMIOS
SUMA Y RESTA DE POLINOMIOS

BINOMIOS

binomios conjugados
- para resolverlo bastara con elevar al cuadrado del primer termino menos el cuadrado del segundo termino
y como su nombre lo indica serán exactamente igual tanto en coeficiente como en exponente lo único que cambiara es el signo
BINOMIOS CONJUGADOS

producto de binomios con termino común
- para resolverlo será igual al cuadrado del termino común mas el termino común que multiplicara a la suma o resta de los términos no comunes mas el producto de los términos no comunes
- Y como su nombre lo indica tendran al menos un termino comun coeficiente o literal
BINOMIOS CON TERMINO COMUN

producto de binomios con termino no común
son aquellos en donde los términos son diferentes y será igual a multiplicar el primer termino del primer binomio por cada uno de los términos del segundo binomio mas el segundo termino del primer binomio se multiplicara a los términos del segundo binomio
y como su nombre lo indica ningún termino es igual todos son completamente diferentes

binomio al cuadrado
- será igual al cuadrado del primer termino mas el doble el producto del primer termino por el segundo mas el cuadrado del segundo termino
BINOMIO AL CUADRADO

SUCESIONES ARITMETICAS

PROGRESION ARITMETICA





SEGUNDO PARCIAL RAZON ARITMETICA Y GEOMETRICA

RAZON ARITMETICA Y GEOMETRICA

PROPORCION GEMOTRICA Y ARITMETICA



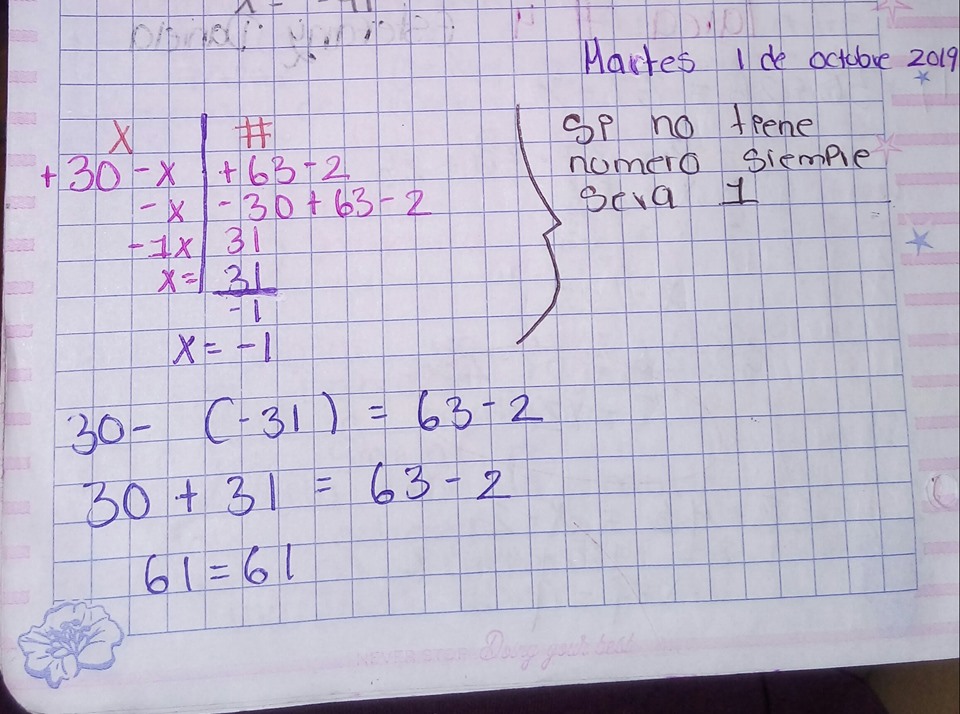


PROPORCION INVERSA Y DIRECTA

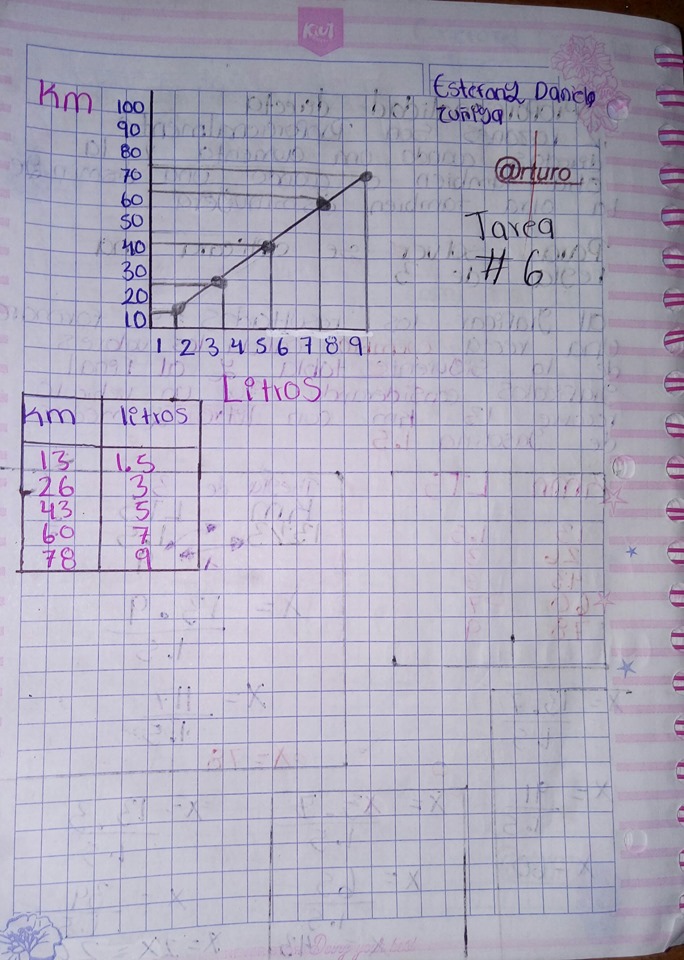


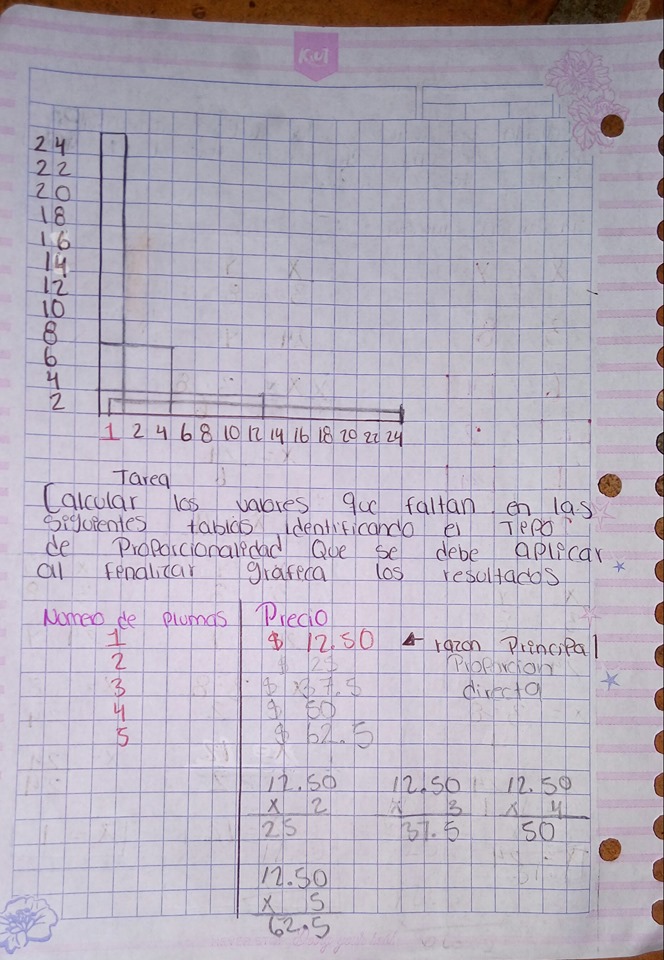

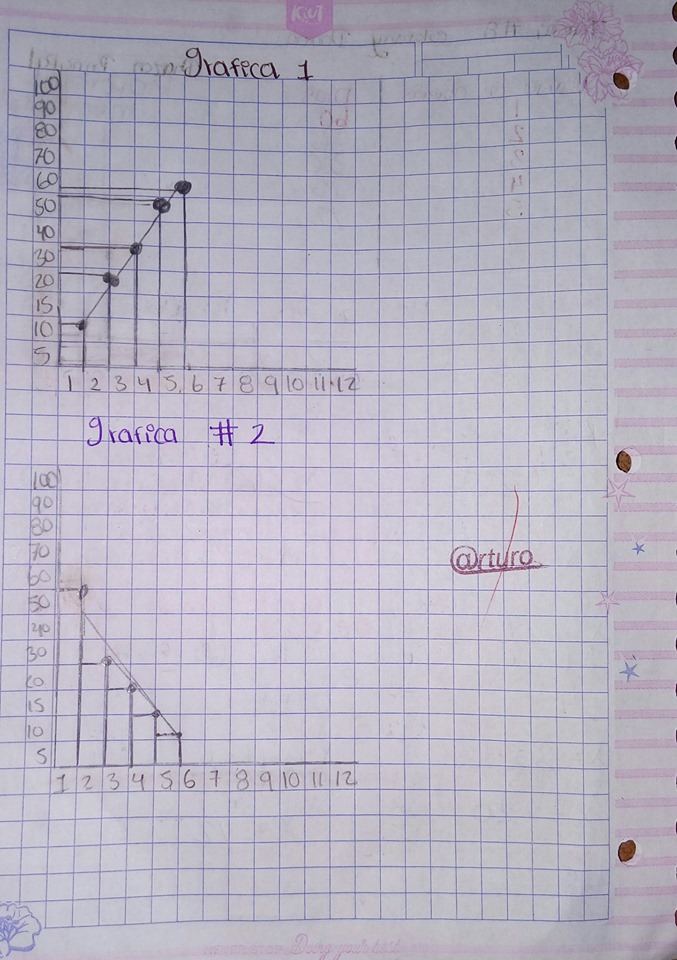
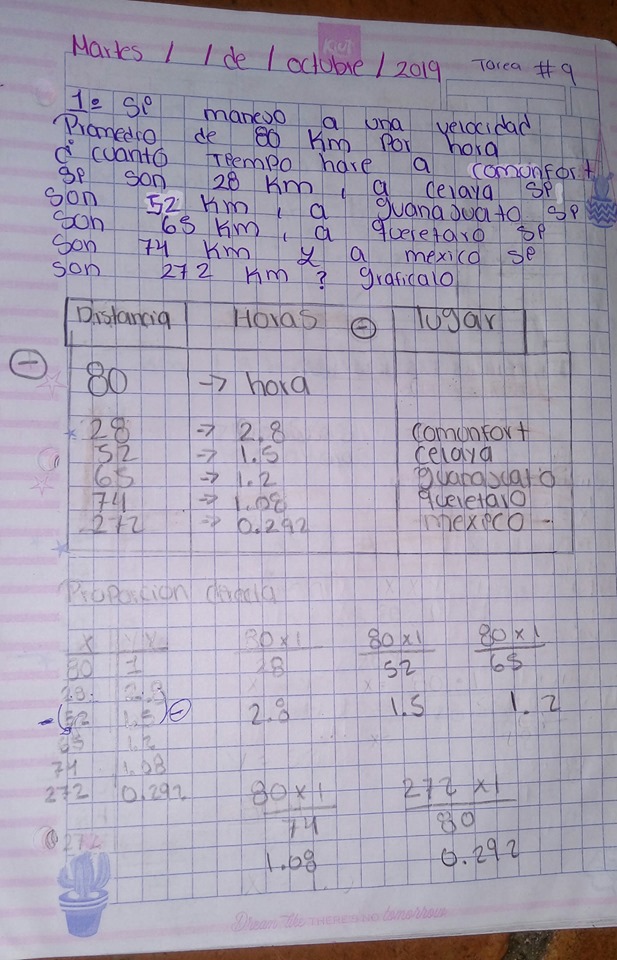

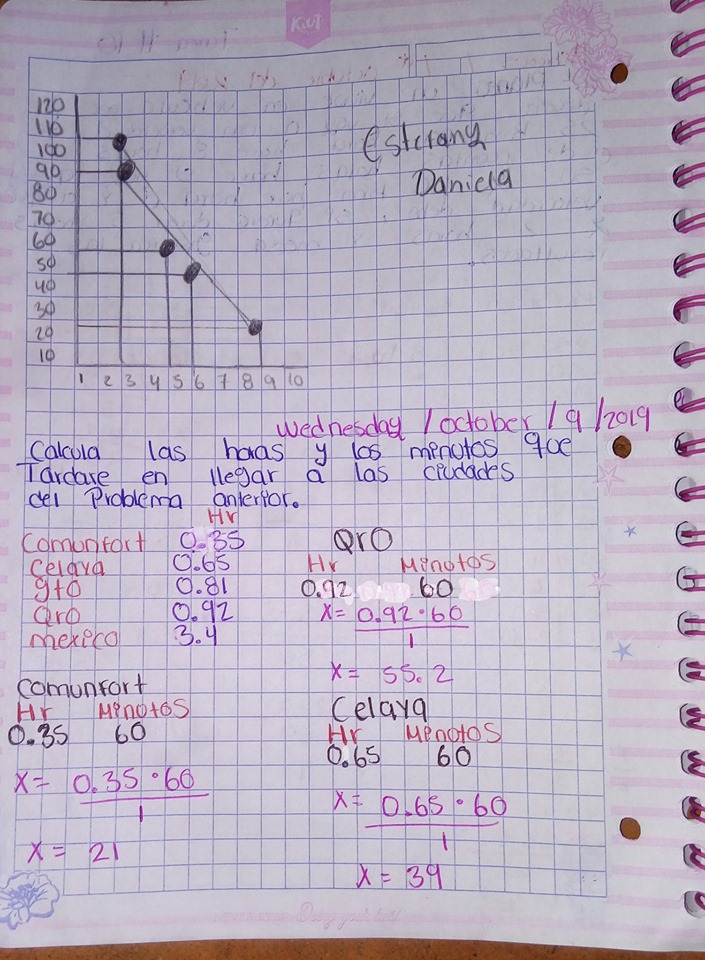
PORCENTAJES









í